KMP 算法核心思想为:通过为模式串建立失败链接,使主串在匹配时不需要回溯索引。
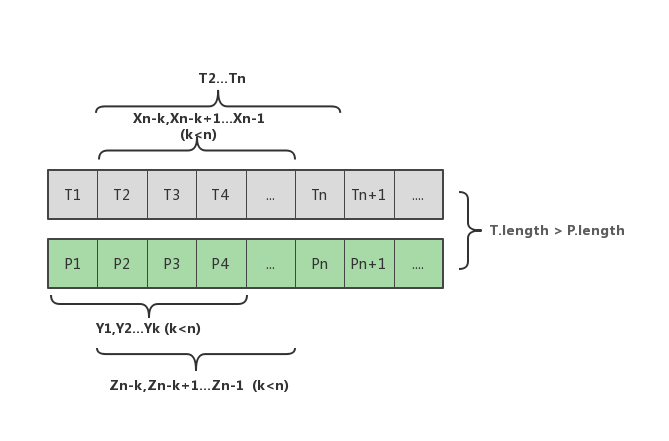
T 为主串,P 为模式。当 P 在 Pn 匹配失败的时候,此时 P1 需要从 T2…Tn 范围内重新开始匹配,假设匹配了 Xn-k,Xn-k+1...Xn-1,则此时 Xn-k,Xn-k+1...Xn-1 == Y1,Y2...Yk,则必然有 Zn-k,Zn-k+1...Zn-1 == Y1,Y2...Yk。X1 的位置并不一定等于 T2,根据此原理,当模式 P 在 n 位置匹配失败的时候,应该使用 Yk+1 位置继续匹配,而主串 T 不需要移动位置。
KMP算法的核心即计算 Yk+1 的值,此值为下标 n 的失败链接值。
String.prototype.searchStr = function(p){
var i = 0,j = 0;
var flink = getFlink(p);
while( i < this.length && j<p.length){
//如果字符相等,或者是模式的第一个字符,主串和模式都应该向后移动一个位置
if(this[i] == p[j] || j==-1){
i++;
j++;
}else{ // 查找失败,只需移动模式串的位置,不需要i回溯
j = flink[j];
}
}
if(j==p.length){ //匹配成功,返回模式串在子串开始的索引下标
return i-p.length;
}else{ //匹配失败,返回-1
return -1;
}
}
//KMP 算法核心(获取失败连接数组)
function getFlink(p){
var flink = [-1,0]; //为-1是为了标记第一个位置(方便之后使用flink去匹配)
for(var i=2; i<p.length; i++){
var preFlink = flink[i-1];
//循环寻找初始子串(从0开始的子串),这个初始子串与以 i-1 字符结尾的子串相匹配
while(preFlink >-1 && p[i-1]!=p[preFlink]){ //aabaaac
preFlink = flink[preFlink];
}
flink[i] = preFlink+1;
}
return flink;
}

