贝塞尔曲线
Bezier curve(贝塞尔曲线)是应用于二维图形应用程序的数学曲线。
曲线定义:起始点、终止点(也称锚点)、控制点。通过调整控制点,贝塞尔曲线的形状会发生变化。
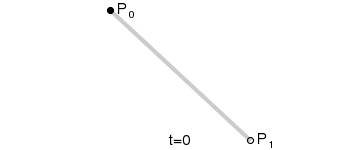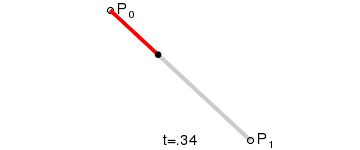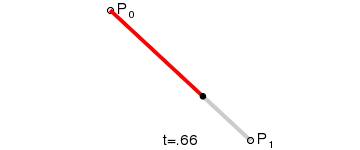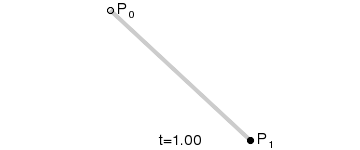
一阶贝塞尔曲线
公式:P01 = (1-t)*P1 + t*P1 ,t∈[0,1]
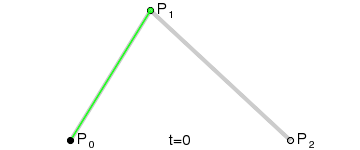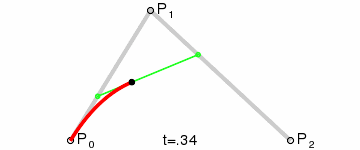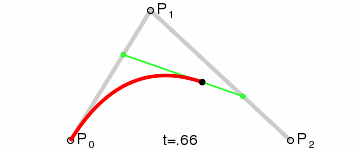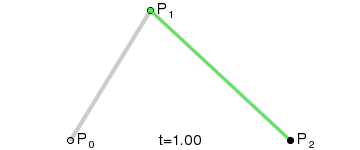
二阶贝塞尔曲线
公式:P02 = (1-t)2*P0 + 2*t*(1-t)*P1 + t2*P2 ,t∈[0,1]
三阶贝塞尔曲线
公式:P03 = (1-t)3*P0 + 3*t*(1-t)2*P1 + 3*(1-t)*t2*P2 + t3*P3 ,t∈[0,1]
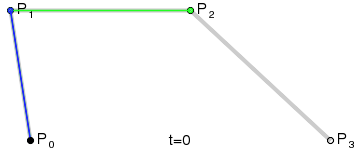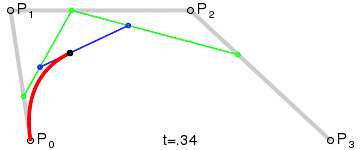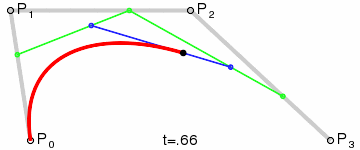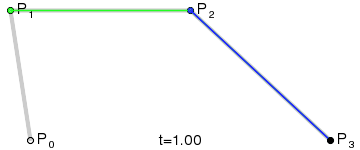
通用公式
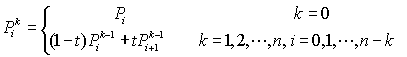
css3动画速度控制 cubic-bezier (x1,y1,x2,y2)
CSS3动画速度的控制通过三次贝塞尔曲线函数实现,定义规则为 cubic-bezier (x1,y1,x2,y2)
cubic-bezier 通过控制曲线上的四个点(起始点、终止点以及两个相互分离的中间点)来创造、编辑图形,绘制出一条光滑曲线并以曲线的状态来反映动画过程中速度的变化。
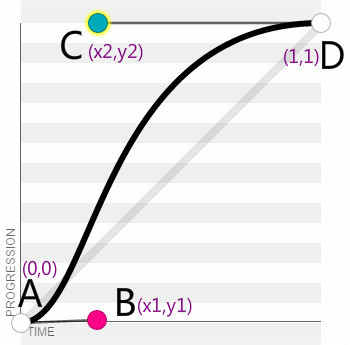
分别用 A,B,C,D 表示这四个点,其中起始点固定值为 A(0,0),终止点固定为 D(1,1)剩下的中间点 B(x1,y1),C(x2,y2) 也就是所要动态操控的两个点了,对应 cubic-bezier(x1,y1,x2,y2) 中的四个参数,通过改变 B,C 两点的坐标值来动态生成一条贝塞尔曲线表示动画中的速度变化。
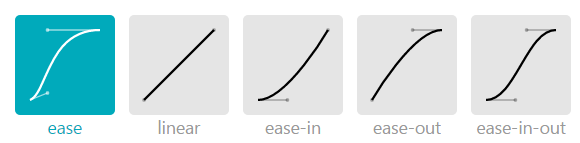
常用的缓动函数参数
| name | cubic-bezier |
|---|---|
| ease | .25,.1,.25,1 |
| linear | 0,0,1,1 |
| ease-in | .42,0,1,1 |
| ease-out | 0,0,.58,1 |
| ease-in-out | .42,0,.58,1 |
Javascript 画三次贝塞尔曲线
<!DOCTYPE html>
<html>
<head>
<title>cubic-bezier</title>
<style type="text/css">
canvas{
transform: rotateX(180deg);
background: red;
}
</style>
</head>
<body>
<canvas width="300" height="300"></canvas>
<script type="text/javascript">
//贝塞尔公式
function bsr(t,p1,p2){
var p0 = 0, p3 = 1;//起点为0,终点为1
//3阶贝塞尔曲线公式
var result = p0*Math.pow((1-t),3) + 3*p1*t*Math.pow((1-t),2) + 3*p2*(1-t)*Math.pow(t,2) + p3*Math.pow(t,3);
return result;
}
//cubic-bezier(.25,.1,.25,1)
function ease(t){
var xScale = bsr(t,0.25,0.25);
var yScale = bsr(t,0.1,1);
var obj = {
xScale: xScale,
yScale: yScale
};
return obj
}
function draw(x1,y1,x2,y2,duration){
var startTime=Date.now();
var ctx = document.querySelector('canvas').getContext('2d');
var preX=x1, preY=y1;
_draw();
function _draw(){
requestAnimationFrame(function(){
var t = (Date.now()-startTime)/duration; //t∈[0,1]
if(t>1){
return;
}
var scale = ease(t);
var x = (scale.xScale*(x2-x1))>>0;
var y = (scale.yScale*(y2-y1))>>0;
ctx.beginPath();
ctx.moveTo(preX,preY);
ctx.lineTo(x,y);
ctx.stroke();
preX = x;
preY = y;
_draw();
})
}
}
draw(0,0,300,300,3000);
</script>
</body>
</html>
结果
Javascript 实现 cubic-bezier 缓动效果
在 css3 中,如果动画定义了 cubic-bezier,则动画所做的事情就是把 x 轴当做时间比例,根据曲线得到 y 轴对应的值(这个 y 值代表了动画的完成度),并更新到动画对象中去。
即转化为以下问题:如何根据上述公式在已知 x 的情况下如何得到 y。
由上面的公式可知,已知 t 的情况下,可以计算出 x 和 y,因此最终问题转换程如何 在已知 x 的情况下 获得 t,也即解一元三次方程。解三次方程常用方法为牛顿迭代法,如果牛顿迭代发解不出可以用二分法来解。
不过还有更简单的方法,可以将 t 分成1000份,计算每一份所对应的 x,y 并保存到数组,之后只要根据 x 找到数组中最接的 x,即可直接获得 y。
<!DOCTYPE html>
<html>
<head>
<title>cubic-bezier</title>
<style type="text/css">
.div{
width: 700px;
height: 100px;
margin-bottom: 10px;
}
.div .bar{
width: 100px;
height: 100px;
background: red;
transform: translateZ(0);
transition: transform 3s;
transition-timing-function: cubic-bezier(.42,0,.58,1);
opacity: 0;
}
.bar.ani{
opacity: 1;
transform: translate3d(600px,0,0);
}
</style>
</head>
<body>
<div class="div"><div class="bar"></div></div>
<canvas width="700" height="100" id="canvas"></canvas>
<script type="text/javascript">
//贝塞尔公式
function bsr(t,p1,p2){
var p0 = 0, p3 = 1;//起点为0,终点为1
//3阶贝塞尔曲线公式
var result = p0*Math.pow((1-t),3) + 3*p1*t*Math.pow((1-t),2) + 3*p2*(1-t)*Math.pow(t,2) + p3*Math.pow(t,3);
return result;
}
var scaleArr = [];
//计算并保存贝塞尔曲线坐标
function caculate(){
for(var i=0; i<=1; i+=0.001){
var xScale = bsr(i,.42,.58);
var yScale = bsr(i,0,1);
var obj = {
xScale: xScale,
yScale: yScale
};
scaleArr.push(obj);
}
}
//根据x坐标获取y坐标
function solve(xScale){
var diff = 1;
var result = 0;
for(var i=0; i<1000; i++){
var _x = scaleArr[i].xScale;
var _diff = Math.abs(_x-xScale);
if(_diff < diff){
diff = _diff;
result = scaleArr[i].yScale;
}
}
return result;
}
function draw(x1,y1,x2,y2,duration){
var startTime=Date.now();
var ctx = document.querySelector('#canvas').getContext('2d');
var diff = duration/1000;
var start = Date.now();
_draw(); //canvas动画
document.querySelector('.bar').className = 'bar ani'; //css3动画
function _draw(){
requestAnimationFrame(function(){
var xScale = (Date.now()-start)/duration; //x轴时间变量,xScale∈[0,1]
if(xScale > 1){
return;
}
var yScale = solve(xScale); //动画完成度
var x = (yScale*(x2-x1)+x1)>>0; //x轴动画完
var y = (yScale*(y2-y1)+y1)>>0; //y轴动画
ctx.clearRect(0,0,800,300);
ctx.fillRect(x,y,100,100); //画矩形
_draw();
})
}
}
caculate();
setTimeout(function(){
draw(0,0,600,0,3000); //画矩形
},60)
</script>
</body>
</html>
结果

从结果可以看出,只要贝塞尔参数相同,用 javascript 可以实现和 css3 相同的效果。
参考:

